Λούβρο: Το μαθηματικό πρόβλημα της δεκαετίας του 1970 που θα μπορούσε να αποτρέψει την «κλοπή του αιώνα»


H παράτολμη κλοπή στο Λούβρο μέρα – μεσημέρι συγκλόνισε όχι μόνο τη Γαλλία, αλλά ολόκληρο τον πλανήτη. Μέσα σε μόλις οκτώ λεπτά, δηλαδή 480 δευτερόλεπτα, οι κλέφτες μπήκαν στο διάσημο μουσείο και έφυγαν με λεία που ξεπερνά τα 86 εκατομμύρια ευρώ.
Τόσο χρόνο χρειάστηκαν οι κλέφτες για να ανέβουν με μία μηχανική πλατφόρμα και να φτάσουν σε ένα μπαλκόνι του πρώτου ορόφου, πριν εισβάλουν στο μουσείο του Λούβρου μέσα από ένα παράθυρο στο φως της ημέρας, να σπάσουν δύο γυάλινες προθήκες και στη συνέχεια να δραπετεύσουν με οκτώ ανεκτίμητα κοσμήματα του στέμματος της εποχής του Ναπολέοντα.
Επτά ύποπτοι έχουν συλληφθεί για την επονομαζόμενη «κλοπή του αιώνα»! Ένα από τα επίμονα ερωτήματα που ακολουθούν την έρευνα για την κλοπή, ωστόσο, είναι γιατί οι κλέφτες δεν εντοπίστηκαν νωρίτερα.

Ένα μαθηματικό πρόβλημα 52 ετών θα έδινε τη λύση
Ενώ δεν υπάρχει αμφιβολία ότι η σύγχρονη ασφάλεια των μουσείων είναι μία περίπλοκη και δαπανηρή υπόθεση, υπάρχει, επίσης, ένα ενδιαφέρον μαθηματικό πρόβλημα 50 ετών που ασχολείται με αυτό ακριβώς το ζήτημα, αναφέρει σε άρθρο του στην ιστοσελίδα του BBC, ο Kit Yates, καθηγητής μαθηματικών και συγγραφέας.
Το εν λόγω πρόβλημα, ρωτάει, ποιος είναι ο ελάχιστος αριθμός φρουρών – ή ισοδύναμα κάμερες CCTV 360 μοιρών – που απαιτούνται για να διατηρείται ένα ολόκληρο μουσείο υπό παρακολούθηση; Είναι γνωστό ως το πρόβλημα του μουσείου ή το πρόβλημα της γκαλερί τέχνης. Η λύση είναι εκλεπτυσμένη.
Αν υποθέσουμε ότι όλοι οι τοίχοι ενός φανταστικού μουσείου είναι ευθείες γραμμές, έτσι ώστε η κάτοψη να είναι αυτό που οι μαθηματικοί ονομάζουν πολύγωνο, ένα σχήμα με σκληρές άκρες και γωνίες. Οι κάμερες πρέπει να βρίσκονται σε σταθερές θέσεις, αλλά μπορούν να βλέπουν προς όλες τις κατευθύνσεις. Για να διασφαλίσουμε ότι καλύπτεται ολόκληρο το μουσείο, θα πρέπει να μπορούμε να σχεδιάσουμε μια ευθεία γραμμή από οποιοδήποτε σημείο της κάτοψης προς τουλάχιστον μία από τις κάμερες.
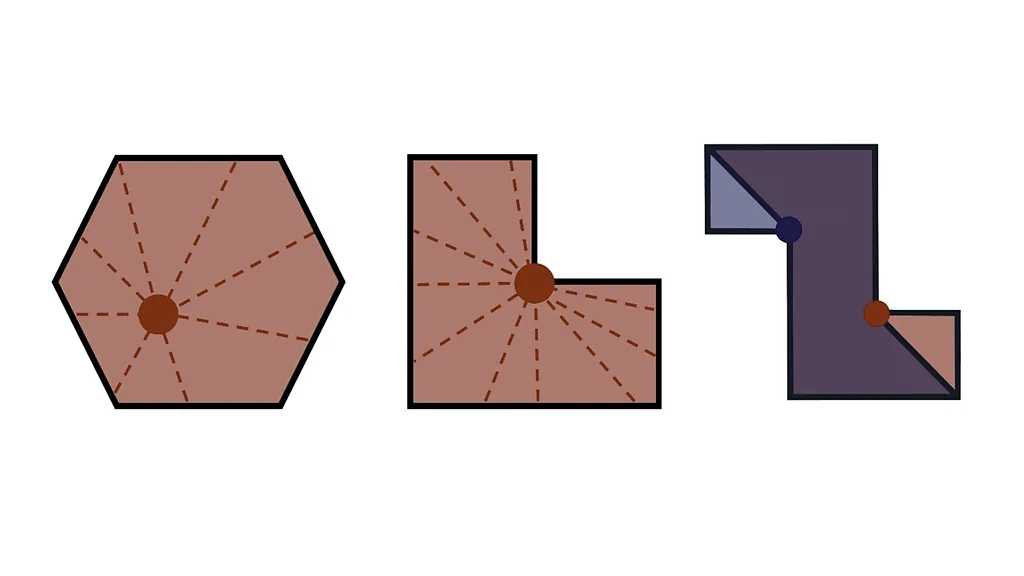
Παίρνοντας σαν παράδειγμα την εξάγωνη γκαλερί στα αριστερά του παρακάτω διαγράμματος.
Ανεξάρτητα από το πού τοποθετείτε την κάμερα, θα μπορείτε να βλέπετε το δάπεδο και τους τοίχους ολόκληρου του χώρου. Όταν κάθε θέση μπορεί να είναι ορατή από κάθε άλλη με αυτόν τον τρόπο, ονομάζουμε το σχήμα της γκαλερί κυρτό πολύγωνο. Η γκαλερί σε σχήμα L στη μέση δεν είναι κυρτή, πράγμα που σημαίνει ότι έχετε περιορισμούς στην τοποθέτηση της κάμεράς σας, αλλά μπορούμε ακόμα να βρούμε σημεία από όπου μια μόνο κάμερα μπορεί να δει όλη τη γκαλερί. Μια γκαλερί σε σχήμα Ζ χρειάζεται δύο κάμερες για να την καλύψει – υπάρχουν πάντα σημεία που μία μόνο κάμερα θα χάσει.
Για πιο ενδιαφέρουσες κατόψεις (δείτε την ασυνήθιστη κάτοψη 15 πλευρών παρακάτω) είναι πολύ πιο δύσκολο να γνωρίζουμε πόσες κάμερες θα χρειαστούν ή πού πρέπει να τοποθετηθούν. Ευτυχώς για τους διευθυντές μουσείων που έχουν οικονομικές δυσκολίες, ο θεωρητικός γραφημάτων Václav Chvátal έλυσε το πρόβλημα του μουσείου σε γενικές γραμμές αμέσως μετά την τοποθέτησή του το 1973.
Η απάντηση, όπως αποδεικνύεται, εξαρτάται από τον αριθμό των γωνιών (ή, όπως τις αποκαλούν οι μαθηματικοί, ”κορυφών”), καθώς θα υπάρχουν τόσοι τοίχοι όσες και οι γωνίες σε ένα δωμάτιο. Μια απλή διαίρεση μας βοηθά να υπολογίσουμε πόσες κάμερες χρειάζονται.
Διαιρώντας τον αριθμό των γωνιών σε ένα δωμάτιο με το τρία, θα μας πει πόσες κάμερες χρειάζονται για να το καλύψουν, υποθέτοντας ότι έχουν ένα πλήρες οπτικό πεδίο 360 μοιρών. Αυτό λειτουργεί ακόμη και για σύνθετα σχήματα όπως η παράξενη γκαλερί 15 πλευρών παρακάτω. Σε αυτήν την περίπτωση υπάρχουν 15 γωνίες, επομένως το 15 δια το τρία ισούται με πέντε.

Αυτό λειτουργεί ακόμη και αν ο αριθμός των γωνιών δεν διαιρείται με το τρία. Για μια γκαλερί 20 πλευρών, για παράδειγμα, η απάντηση είναι έξι και δύο τρίτα. Σε αυτές τις περιπτώσεις μπορείτε να πάρετε τον ακέραιο αριθμό – επομένως δεν θα χρειαζόμασταν ποτέ περισσότερες από έξι κάμερες σε ένα δωμάτιο 20 πλευρών.
Το 1978, ο Steve Fisk, καθηγητής μαθηματικών στο κολέγιο Bowdoin στο Μέιν των ΗΠΑ, κατέληξε σε μία απόδειξη – που θεωρείται μία από τις πιο εκλεπτυσμένες σε όλα τα μαθηματικά – αυτού του κατώτερου ορίου στον αριθμό των καμερών που χρειάζονται.
Η στρατηγική του ήταν να χωρίσει τη γκαλερί σε τρίγωνα (δείτε την αριστερή εικόνα του παρακάτω σχήματος). Στη συνέχεια, απέδειξε ότι μπορείτε να επιλέξετε μόνο τρία χρώματα – ας πούμε κόκκινο, κίτρινο και μπλε – και να αντιστοιχίσετε ένα διαφορετικό χρώμα στις γωνίες κάθε τριγώνου. Αυτό θα σήμαινε ότι κάθε τρίγωνο στη γκαλερί σας έχει ένα διαφορετικό χρώμα στις τρεις γωνίες του (δείτε τη δεξιά εικόνα του παρακάτω σχήματος για ένα παράδειγμα). Αυτό είναι γνωστό ως «βάφοντας με τρία χρώματα» τις γωνίες.
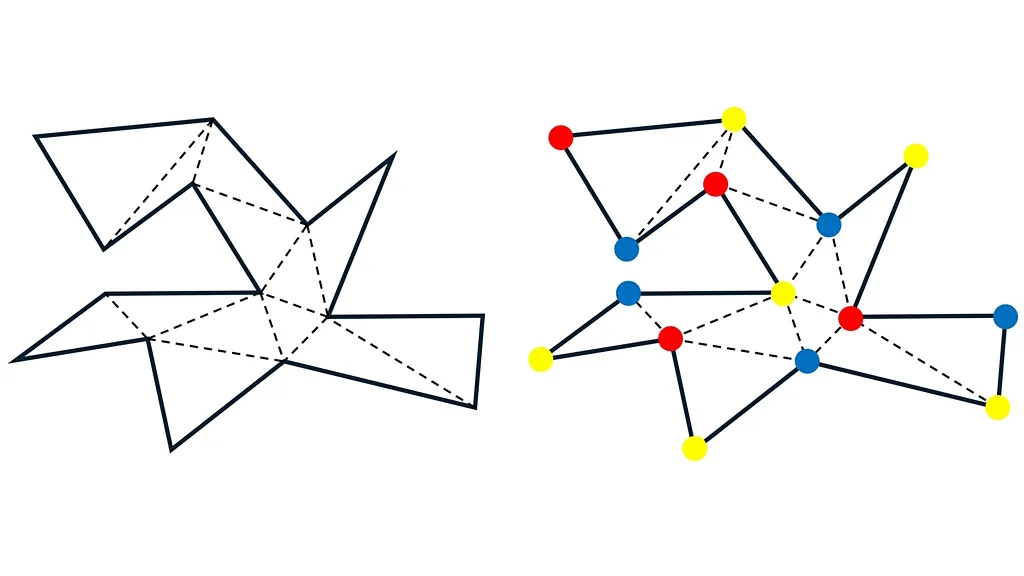
Τα τρίγωνα είναι ένα από αυτά τα ”κυρτά” πολύγωνα που αναφέρθηκαν νωρίτερα, επομένως μία κάμερα τοποθετημένη σε οποιαδήποτε γωνία (ή και οπουδήποτε στο τρίγωνο) μπορεί να δει κάθε σημείο σε αυτό το σχήμα. Κάθε τρίγωνο έχει γωνίες με καθένα από τα τρία χρώματα. Αυτό σημαίνει ότι μπορείτε να επιλέξετε μόνο ένα από τα χρώματα και να τοποθετήσετε κάμερες σε αυτές τις θέσεις. Αυτές οι κάμερες θα μπορούν να δουν κάθε μέρος κάθε τριγώνου, και επομένως κάθε μέρος της γκαλερί. Αλλά εδώ είναι το καλύτερο μέρος.
Η ομορφιά της απόδειξης του Fisk είναι ότι μπορείτε απλώς να επιλέξετε το χρώμα με τις λιγότερες κουκκίδες, και θα καλύψετε ακόμα ολόκληρη τη γκαλερί. Στο σχήμα 15 πλευρών παραπάνω, επιλέγοντας τις κόκκινες κουκκίδες, μπορούμε να τη γλιτώσουμε με μόνο τέσσερις κάμερες.
Στην πραγματικότητα, η κόκκινη κουκκίδα επάνω αριστερά δεν είναι απαραίτητη, επειδή η επόμενη κόκκινη κάμερα μπορεί να καλύψει ολόκληρο τον χώρο επιτήρησής της. Έτσι, θα μπορούσαμε ακόμη και να τη γλιτώσουμε με τρεις κάμερες για αυτήν τη γκαλερί. Αυτό ισχύει ιδιαίτερα αν προσαρμόζαμε σύγχρονες πανκατευθυντικές κάμερες, αντί για τις παλιές, ευρυγώνιες ροές CCTV που θα έπρεπε να σαρώνουν μια περιοχή για να παρέχουν πλήρη κάλυψη, δημιουργώντας προσωρινά «τυφλά» σημεία.
Αξίζει όμως να θυμόμαστε ότι πολλά παραδοσιακά μουσεία όπως το Λούβρο έχουν ως επί το πλείστον ορθογώνιες αίθουσες. Ευτυχώς, μια παραλλαγή του προβλήματος της γκαλερί τέχνης δείχνει ότι όταν οι τοίχοι συναντώνται σε ορθή γωνία, χρειαζόμαστε μόνο μία κάμερα για να καλύψουμε ολόκληρο το δωμάτιο.

Στην κατάθεσή της, η Des Cars, η Γαλλίδα ιστορικός τέχνης και διευθύντρια του Μουσείου του Λούβρου, αναγνώρισε, επίσης, ότι οι περιμετρικές κάμερές του δεν καλύπτουν όλους τους εξωτερικούς τοίχους. «Δεν εντοπίσαμε την άφιξη των κλεφτών αρκετά νωρίς… η αδυναμία της περιμετρικής μας προστασίας είναι γνωστή», είπε.
Ευτυχώς, υπάρχουν εκδοχές του προβλήματος, γνωστές ως «το πρόβλημα του φρουρίου» ή «το πρόβλημα της φυλακής», που λύνουν και το πρόβλημα κάλυψης της κάμερας για το εξωτερικό ενός κτηρίου.
Αυτό που αποκαλύπτουν και οι δύο παραλλαγές, ωστόσο, είναι ότι η εύρεση των κατάλληλων σημείων θέασης είναι απαραίτητη. Αλλά είναι σημαντικό να αναγνωρίσουμε ότι οι κλέφτες που εισέρχονται μέσω δημόσιων στοών δεν αποτελούν τη μόνη απειλή που αντιμετωπίζουν τα μουσεία. Παράλληλα με την κλοπή, τα μουσεία πρέπει επίσης να προστατεύουν τις συλλογές τους από βανδαλισμούς, πυρκαγιές και άλλες μορφές καταστροφής.
To άρθρο Λούβρο: Το μαθηματικό πρόβλημα της δεκαετίας του 1970 που θα μπορούσε να αποτρέψει την «κλοπή του αιώνα» δημοσιεύτηκε στο NewsIT .




